
Watch it together with the written tutorial to deepen your understanding: Starting With Linear Regression in Python This means that, on average, when the number of drinks increases by 1, we expect the reaction to increase by approximately 9.7cm.Watch Now This tutorial has a related video course created by the Real Python team. This means that, on average, we expect the reaction to be approximately 11.3cm when the participant has had 0 drinks. We communicate that using words like “approximately” and “on average” and “we expect.” However, we have to remember that we are summarizing the behavior of distributions. These have a similar interpretation in the statistical world.
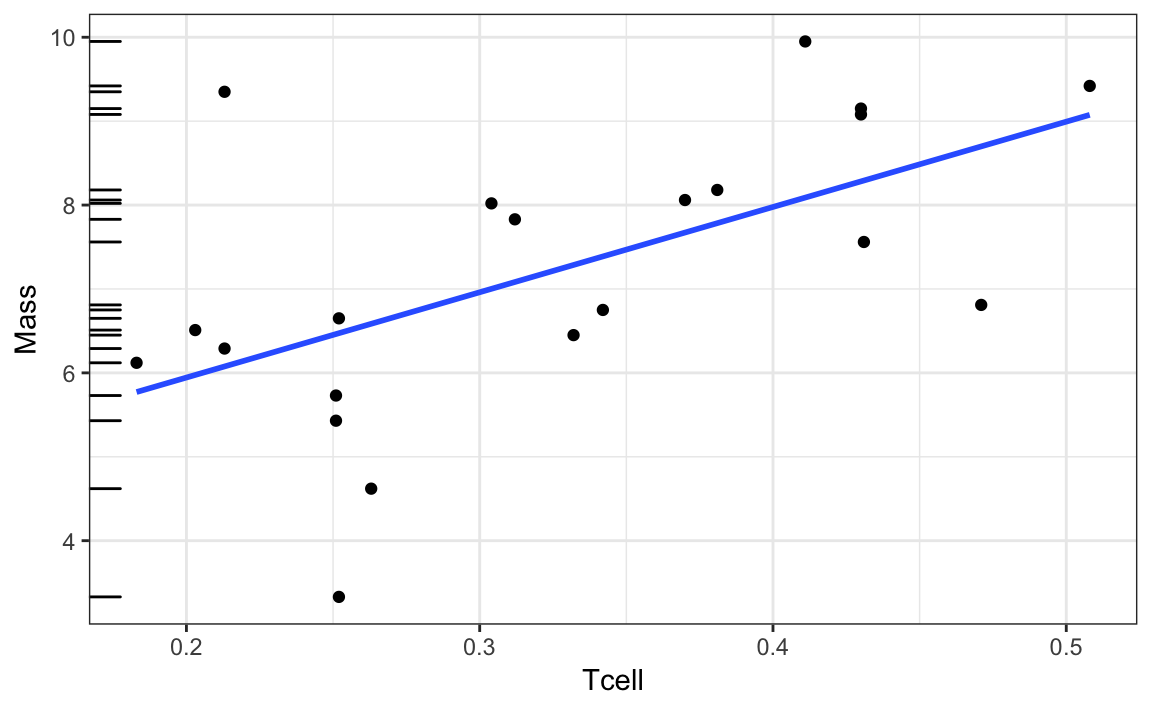
Just like in the mathematical world, there is an intercept and a slope. This means that the line is not biased towards overestimating the means or underestimating the means. The linear regression line balances these deviations (if you add up the red deviations, it would be equal to the blue deviations). The deviations from the line to the means are marked in red and blue. Notice that the line doesn’t fit the mean of the distributions perfectly, but it’s pretty close. 5.5 Activity: Statistical estimates in the newsįigure 1.19: A linear regression line for alcohol and reaction time.5.4 Activity: Comparing cuddling preferences.5.3 Activity: Comparing statistical estimates (part 2): Sample size.

5.1 Activity: Crazy in love (part 2): Sample size and population size. 4.8 Activity: Comparing statistical estimates. 4.6.1 Quantification of Uncertainty: Margin of Error. 4.6 Compatibility intervals and margin of error. 4.5 Activity: Monday breakups revisited. 4.4 Activity: Validity evidence: Studies of Peanut Allergies. 4.2 External Validity Evidence and Random Sampling. 4 Random sampling, generalization, and statistical estimation. 3.11 Review activity: Gender coding and expectations. 3.9.2 Drawing causal inferences from observational studies. 3.9.1 Hypothesis tests for observational studies. 3.9 Observational Studies vs. Experiments. 3.7 Activity: Internal validity evidence. 3.6.1 Example: Does sleep deprivation cause an decrease in performance?. 3.5 Activity: Stereotypes and creativity. 3.2 Random assignment and experimental variation. 3 Comparing two groups: Experiments, observational studies, and causation (internal validity). 2.16 Review activity: Racial disparities in police stops. 2.14.3 Other things that statistical significance can’t tell us. 2.14.2 Statistical significance vs. practical significance. 2.14 Drawing conclusions and “statistical significance”. 2.12.1 Adjustment for Simulation Results. 2.10 A closer look at statistical hypothesis testing. 2.7.1 Simulation Process for Evaluating Hypotheses. 2.7 Introduction to statistical hypothesis testing. 2.6 Activity: Montana political parties. 2.5.1 How many trials do you need to run?. 2.4.3 Automating the simulation process. 2.4.2 Monte Carlo Simulation 2: Generating a Sample of Students. 2.4 Activity: Building Monte Carlo simulations. 2.3.3 Monte Carlo Simulation in Practice. 2.3.2 Monte Carlo Simulation Assumptions. 2.3.1 Example of a Monte Carlo Simulation Study. 2 Introduction to modeling, simulation, and hypothesis testing. 1.8.2 Summarizing a liner assocation in a statistical world. 1.8.1 Summarizing a liner assocation in a mathematical world. 1.7.3 Describing statistical association. 1 Introduction to data, variation, and distributions. Statistical Thinking: A Simulation Approach to Modeling Uncertainty (STAT 216 edition).







 0 kommentar(er)
0 kommentar(er)
